Barrier free Colours according to DIN 32975

Which colour combinations are barrier free?

A DIN standard has only existed since 2009 for the "Design of visual information in public space for barrier free use." It governs the colours of certain elements in areas open to public use, e.g. swimming pools, streets, town halls, private Inns, beer gardens, camping sites, hotels,...

The standard is also supposed to supply visually impaired individuals with a risk free stay in public. It is always to be complied with when a building is to be desginated as "barrier-free". In multiple cases the public sector required themselves to do so. Often times there are also national building codes in which compliance is required from private builders building in public sectors.

Requirements and their Calculations

The norm of standard colouring concerns important elements that one has to recognize immediately in order to move around and/or manipulate therein safely. On one hand the so called "operating controls" e.g. handels, knobs and buttons on doors or vending machines are regulated on the other hand so are "orientation elements" such as marking of roads, signage and display panels.

For these elements it is necessary that they display a minimal contrast of 0.4 from the surrounding environment.

An elevated minimal contrast of 0.7 is required for:

The minimal contrast is calculated, according to the norm, using the so called Michelson formula. For this the luminosity Y of both colours is defined as having the following relationship: K=(Y2-Y1)/(Y2+Y1)

The contrast simply results from both luminosity values. The colour itself and its intensity (saturation) are left out. A pure colour contrast e.g. red-green with as much luminosity as possible does not conform to standards. This makes perfect sense if one considers that approximately 1 in 20 humans (predominantly men) are red/green colour blind. Although absolute colour blindness is quite rare there are numerous prevalent weaknesses in colour perception.

In German vernacular there is a saying "At night all cats are grey". In other words: Even those with normal sight can recognize neither colour nor saturation differences in the dark. Since we would still like to be able to move about safely the foundation of the norm on brightness contrasts is sensible.

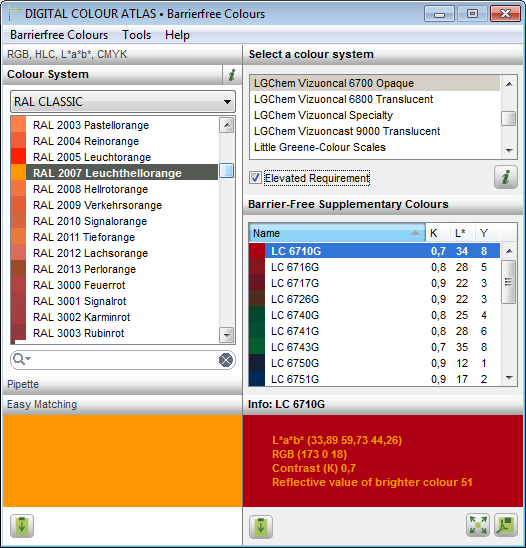
Sufficiently contrasting colours are calculated for a given colour according to regulations.

Brief Instruction

  1. Select the input colour from the left side.
  2. Indicate on the right side whether the element has elevated demands (Kmin = 0.7) or whether it is a general orientation and operating element (Kmin = 0.4).
  3. The appropriate complementary colours will be displayed in a list.
  4. Click on a colour in the list in order to obtain further information. You can save this list as a PDF file.

Michelson formula, Illumination, Luminous Density and Luminosity

The DIN 32975 actually sets the so called luminous density of two surfaces into correlation with the above mentioned Michelson-Formula: K=(L2-L1)/(L2+L1)

The luminous density is a measurement for the intensity of the luminous flux that originates from a square meter of an illuminated surface. It is measured in Candela by square meter and is e.g. very high with the sun in a daytime sky (1.6 billion cd/m²), lesser with a lightbulb (120,000 cd/m²) or with the average overcast sky (2,000 cd/m²). The following applies: The smaller or the brigher a light source the higher the luminous density.

Candela is the measure for illumination and was originally defined as the "incidence of light in a 1 meter distance that is generated by a candle, that uses 7.77 g spermaceti per hour". These days candles are luckily no longer made from Whales, and the definition of the illumination is (unfortunately) not clear: "A light source has 1 cd luminosity in any spatial direction, when it creates the same signal on a sensor with standardised spectral sensitivity characteristics of the human eye, as monochromatic light with the frequency 540 – 1012 Hz and the radation intensity of 1/683 W/sr."

The identification and objects that the DIN 32975 is supposed to handle do not deal with light sources, rather we are dealing with colourful surfaces whose luminous intensity is due to reflection properties and the lighting situation. If one inserts the CIE-neutral white as the standard light, then one can also insert the luminosity value Y in the Michelson-formula: K=(Y2-Y1)/(Y2+Y1)

Here standard prerequisites are being met that apply fairly well in the reality of an open room by daylight or in lighting under a continuous or white spectrum.

However the outcome reveals a conceptional weakness of the DIN Norm for public spaces with wide spread out tinted light sources. Following example: Dark paving stones are labelled in signal green (narrow remission spectrum). Now if the labelling is lighted with light that has no green parts (e.g. mercury vapour lamp), then the markings are very visible in daylight and almost invisible in the dark!